Contents
- Вступ
- Підготовка даних і встановлення NetworkX
- Починаємо
- Метрики, доступні в NetworkX
- Експорт даних
- Нарис висновків
Вступ
Цілі уроку
У цьому уроці ви дізнаєтесь:
- Як використовувати пакет NetworkX для роботи з мережевими даними в Python; і
- Як аналізувати дані гуманітарної мережі, щоб знайти:
- Структуру мережі та довжину шляху,
- Важливі або центральні вершини, і
- Спільноти та підгрупи.
Примітка: це урок для вивчення статистики та метрики-показників мережі. Тому ми зосередимося на способах аналізу мереж, не візуалізуючи їх. Ймовірно, вам знадобиться поєднання візуалізації та мережевих метрик-показників у вашому власному проекті, тому ми рекомендуємо цю статтю як додаток до цього попереднього уроку Programming Historian.
Пререквізити
Цей урок передбачає, що у вас є:
- базове знайомство з мережами та/або ви попередньо прочитали «Від герменевтики до даних до мереж: вилучення даних і мережева візуалізація історичних джерел» Мартіна Дюрінґа тут, на Programming Historian ;
- встановлено Python 3, а не Python 2, який попередньо встановлений в операційних системах на базі Unix, наприклад Mac (якщо вам потрібна допомога з інсталяцією Python 3, перегляньте «Посібник автостопом по Python»); і
- встановлено інсталятор пакетів
pip.1
На комп’ютері можна одночасно інсталювати дві версії Python (2 і 3). Тож через це, під час доступу до Python 3 вам часто доведеться вказувати саме його, ввівши python3 і pip3 замість просто python і pip. Перегляньте навчальні посібники Programming Historian щодо встановлення Python і роботи з pip, щоб дізнатися більше.
Що можна дізнатися з мережевих даних?
Мережі вже давно цікавлять дослідників у гуманітарних науках, але багато вчених в останніх дослідженнях перейшли від переважно якісного та метафоричного інтересу в зв’язках і з’єднаннях до більш формального набору кількісних інструментів для вивчення посередників, хабів і взаємопов’язаних структур. Як зазначив соціолог Марк Грановеттер у своїй статті 1973 року «Сила слабких зв’язків», що недостатньо помітити, що дві людини були пов’язані одна з одною. Вирішальний вплив на події мають такі фактори, як їхній структурний зв’язок із іншими людьми та чи були ці «інші люди» також пов’язані між собою. Оскільки навіть найпроникливішим ученим важко зрозуміти, скажімо, загальну форму мережі (її мережеву «топологію») і визначити вершини, найбільш важливі для з’єднання груп, кількісний мережевий аналіз пропонує вченим спосіб відносно плавного переходу між великомасштабним соціальним об’єктом («графом») і дрібними особливостями людей і соціальних зв’язків.
Цей урок допоможе вам відповісти на такі питання, як:
- Яка загальна структура мережі?
- Хто є важливими людьми або хабами в мережі?
- Які є підгрупи та спільноти в мережі?
Наш приклад: деякі міщани, які жили у Львові на зламі XVI-XVII ст.
Маґдебурзьке право міст Східної Європи (Львова зокрема) походить із Заходу, тобто німецьких земель. Одним із найвідоміших німецьких правових збірників з часів Середньовіччя було «Саксонське зерцало», закони якого, за посередництвом праць Бартоломея Ґроїцького, частково вживалися в міських судах Львова. Один зі таких законів передбачав обов’язкове опікунство (представництво) для жінки, неповнолітніх дітей та духовних осіб в суді. Опікуном дружини найчастіше виступав чоловік; вдови — близький родич; дітей — призначені заповідачем або магістратом рідні, побратими по цеху, сусіди; монахів чи кліру — світський провізор монастиря, церкви або інші особи. Представник міг бути призначений на певний період (наприклад, до повноліття чи наступного шлюбу) або для якоїсь конкретної справи (tutor ad rem). Досліджуючи книги протоколів уряду ради Львова періоду 1578-1604 рр. вдалося укласти вибірку учасників судових процесів (жінок, неповнолітніх осіб і духовенства) та їх представників. З допомогою цих даних спробуємо з’ясувати які люди найчастіше ставали опікунами в обраний проміжок часу.
Підготовка даних і встановлення NetworkX
Перш ніж розпочати цей урок, вам потрібно буде завантажити два файли, які разом складають набір мережевих даних. Файл lviv_network_nodes.csv це список жителів ранньомодерного Львова (вершини) та файл lviv_network_edges.csv це список зв’язків між цими людьми (ребра). Щоб завантажити ці файли, просто клацніть посилання правою кнопкою миші та виберіть «Зберегти посилання як…».
Перш ніж продовжити, буде дуже корисно ознайомитися зі структурою набору даних. Щоб дізнатися більше про загальну структуру мережевих наборів даних, перегляньте цей урок. Коли ви відкриєте файл з вершинами у програмі, яку ви оберете, ви побачите, що кожен міщанин в основному ідентифікується за своїм іменем. Кожна вершина також має пов’язаний атрибут - стать. Ось декілька перших рядків:
Name,Gender
Margareta Joannis olim Winiarz ex pl. Temryczowska sbs. Haliciensis vidua,female
"Magister Albertus Pedianus, gener",male
"Catherina de Medinicze Mathiae Kusma conj., filia olim Catherinae Woythkowna qua fuit soror germana Magdae conj. Jacobi Szoszenka Ferrifabri sbs. L.",female
Sophia Armena olim Grzeskonis Jakubowic Armeni cv. L. vidua,female
Palachna Bildachowna Ruthena _ukiani Wasilowic conj. cv. L.,female
Зауважте, що хоча стовпці не вибудовуються правильно, як це відбувається в електронній таблиці, коми все розділяють у відповідному порядку.
Коли ви відкриєте файл з «ребрами», ви побачите, що ми використовуємо імена з файлу вершин для ідентифікації вершин, з’єднаних кожним ребром. Ці ребра починаються у вихідній вершині та закінчуються у цільовій вершині. Хоча ця мова походить від так званих структур спрямованої мережі, ми будемо використовувати наші дані як неспрямовану мережу: якщо особа А знає особу Б, то особа Б також повинна знати особу А. У спрямованих мережах відносини не обов’язково мають бути взаємними (особа A може надіслати лист B, не отримавши його назад), але в неспрямованих мережах з’єднання завжди взаємні або симетричні. Оскільки це мережа тих, хто кого знав, а не, скажімо, мережа листування, неспрямований набір відносин є найбільш підходящим. Симетричні зв’язки в неспрямованих мережах корисні будь-коли, коли ви цікавитеся зв’язками, які мають однакову роль для обох сторін. Два друга пов’язані симетричними стосунками: кожен з них є другом один одному. Автор листів і одержувач мають асиметричні стосунки, оскільки кожен виконує різну роль. Спрямовані та неспрямовані мережі мають свої власні можливості (а іноді й власні унікальні показники), і ви захочете вибрати той, який найкраще відповідає типам стосунків, які наявні в даних, і запитанням, на які ви хочете відповісти. Ось перші кілька ребер у неспрямованій мережі жителів Львова:
Source;Target;Relation
Anastasia Ichnathowa Ruthena;Simon Kinost;tutor
Anastasia Armena olim Nicolai Armeni Hreori olim Domazersky Armeni fratris cv. L. vidua;Simon Kinost;tutor
Martha Ancziporkowna, quondam Stanislai Pellionis sbs. L. vidua;Iwan Bildacha Ruthenus, affinis;tutor
Тепер, коли ви завантажили дані і подивилися, як вони структуровані, настав час почати працювати з цими даними в Python. Після встановлення Python і pip (див. попередні пререквізити вище), вам потрібно інсталювати NetworkX, ввівши це в командний рядок:2
pip3 install networkx==3.0
Нещодавно NetworkX оновлено до версії 3.0. Якщо у вас виникли проблеми з наведеним нижче кодом і ви раніше працювали з NetworkX, ви можете спробувати оновити наведений вище пакет за допомогою pip3 install networkx==3.0 —upgrade.
І це все! Ви готові почати кодити!
Починаємо
Читання файлів, імпорт даних
Запустіть новий порожній файл відкритого тексту в тому самому каталозі, що й ваші файли даних під назвою lviv_network.py (щоб дізнатися більше про встановлення та запуск Python, перегляньте цей урок). У верхній частині цього файлу імпортуйте потрібні бібліотеки. Вам знадобляться три бібліотеки — та, яку ми щойно встановили, і дві вбудовані бібліотеки Python. Ви можете ввести:
import csv
from operator import itemgetter
import networkx as nx
from networkx.algorithms import community # Цю частину networkx, для виявлення спільноти, потрібно імпортувати окремо.
Тепер ви можете дати команду програмі читати ваші CSV файли і отримувати дані, які вам потрібно. За іронією долі, для читання файлів і реорганізації даних переважно потрібен більш складний код, ніж той, що потрібен для функцій, які використовуються для аналізу соціальних мереж, тому, будь ласка, залишайтеся з нами впродовж першого блоку коду. Ось набір команд для відкриття та читання наших файлів nodelist і edgelist:
with open('lviv_network_nodes.csv', 'r', encoding = "utf-8") as nodecsv: # Відрийте файл
nodereader = csv.reader(nodecsv, delimiter= ",") # Прочитайте csv-файл
# Отримайте дані (використовуючи списковий вираз Python і виділення частини списку, щоб видалити рядок заголовка, дивіться виноску 3)
nodes = [n for n in nodereader][1:]
node_names = [n[0] for n in nodes] # Отримайте список лише назв вершин
with open('lviv_network_edges.csv', 'r', encoding = "utf-8") as edgecsv: # Відрийте файл
edgereader = csv.reader(edgecsv, delimiter= ";") # Прочитайте csv-файл
edges = [e for e in edgereader][1:] Retrieve the data
edge_names = [[e[0], e[1]] for e in edges] # Отримайте список лише джерела та цілі ребер
Цей код виконує функції, подібні до тих, що описані в цьому уроці, але використовує модуль CSV для завантаження ваших вершин і ребер. Пізніше ви можете повернутися і отримати більше інформації про вершини, але наразі вам потрібні дві речі: повний список вершин і список пар ребер (як кортежі вершин)3. Це форми, які NetworkX знадобляться для створення «об’єкту графа», спеціального типу даних NetworkX, про який ви дізнаєтеся в наступному розділі.
На цьому етапі, перш ніж почати використовувати NetworkX, ви можете виконати деякі основні перевірки, щоб переконатися, що ваші дані завантажуються правильно за допомогою вбудованих функцій і методів Python. За допомогою команд
print(len(nodes))
та
print(len(edges))
а потім запустивши ваш скрипт коду, ви побачите, скільки вершин і ребер ви успішно завантажили в Python. Якщо ви бачите 150 вершин і 127 ребер, то у вас є всі необхідні дані.
Основи NetworkX: створення графа
Тепер у вас є дані у вигляді двох списків Python: списку вершин node_names і списку ребер edge_names. У NetworkX ви можете об’єднати ці два списки в один мережевий об’єкт, який розуміє, як взаємопов’язані вершини та ребра. Цей об’єкт називається Graph (граф), посилаючись на один із загальних термінів для даних, організованих у вигляді мережі [Примітка. це не стосується жодного візуального представлення даних. Graph тут використовується суто в математичному сенсі мережевого аналізу.] Спочатку ви повинні створити об’єкт Graph за допомогою такої команди:
G = nx.Graph()
Це створить новий пустий об’єкт Graph, G. Тепер ви можете додати свої списки вершин і ребер так:
G.add_nodes_from(node_names)
G.add_edges_from(edge_names)
Це один із кількох способів додавання даних до мережевого об’єкта. Ви можете переглянути документацію NetworkX, щоб отримати інформацію про додавання зважених ребер або додавання вершин і ребер один за одним.
Зрештою, ви можете отримати основну інформацію про свою щойно створену мережу просто вивівши граф4.
print(G)
Результат має виглядати так:
Graph with 149 nodes and 114 edges
Це швидкий спосіб отримати загальну інформацію про ваш граф, але, як ви дізнаєтесь у наступних розділах, це лише верхівка айсбергу того, що NetworkX може розповісти вам про ваші дані. Зауважте, що кількість ребер зменшилась - це через те, що ми маємо повторні рядки вершини-джерела та цільової вершини, однак з різним типом зв’язку, який ми наразі не розпізнаємо.
Підсумовуючи, на даний момент ваш скрипт коду виглядатиме так:
import csv
from operator import itemgetter
import networkx as nx
from networkx.algorithms import community # Цю частину networkx, для виявлення спільноти, потрібно імпортувати окремо.
with open('lviv_network_nodes.csv', 'r', encoding = "utf-8") as nodecsv: # Відрийте файл
nodereader = csv.reader(nodecsv, delimiter= ",") # Прочитайте csv-файл
# Отримайте дані (використовуючи списковий вираз Python і виділення частини списку, щоб видалити рядок заголовка, дивіться виноску 3)
nodes = [n for n in nodereader][1:]
node_names = [n[0] for n in nodes] # Отримайте список лише назв вершин
with open('lviv_network_edges.csv', 'r', encoding = "utf-8") as edgecsv: # Відрийте файл
edgereader = csv.reader(edgecsv, delimiter= ";") # Прочитайте csv-файл
edges = [e for e in edgereader][1:] Retrieve the data
edge_names = [[e[0], e[1]] for e in edges] # Отримайте список лише джерела та цілі ребер
# Виведіть кількість вершин і ребер у наших двох списках
print(len(node_names))
print(len(edge_names))
G = nx.Graph() # Ініціалізуйте об’єкт Graph
G.add_nodes_from(node_names) # Додайте вершини до графа
G.add_edges_from(edge_names) # Додайте ребра до графа
print(G) # Виведіть інформацію про граф
Досі ви зчитували дані вершин і ребер у Python із файлів CSV, а потім підраховували ці вершини та ребра. Після цього ви створили об’єкт Graph за допомогою NetworkX і завантажили свої дані в цей об’єкт.
Додавання атрибутів
Для NetworkX об’єкт Graph — це одний великий об’єкт (ваша мережа), що складається з двох видів менших об’єктів (ваших вершин і ваших ребер). Досі ви завантажували вершини та ребра (як пари вершин), але NetworkX дозволяє додавати атрибути до вершин і ребер, надаючи більше інформації про кожен із них. Пізніше в цьому уроці ви запустите функції для обрахунку метрик та додасте деякі результати назад до Graph як атрибути. Наразі давайте переконаємося, що ваш Graph містить усі атрибути, які зараз є в нашому CSV.
Ви захочете повернутися до списків, який ви створили на початку сценарію: вершини та ребра. Перший список містить усі рядки з lviv_network_nodes.csv, включно з стовпцем для статі, а другий - усі рядки з lviv_network_edges.csv, включно з стовпцем для позначення типу зв’язку. Вам потрібно прокрутити ці список і додати цю інформацію до нашого графа. Є кілька способів зробити це, але NetworkX надає дві зручні функції для додавання атрибутів до всіх вершин або ребер Graph одночасно: nx.set_node_attributes() і nx.set_edge_attributes(). Щоб використовувати ці функції, вам знадобиться, щоб ваші дані атрибутів були у формі словника Python, у якому імена вершин є ключами, а атрибути, які ви хочете додати, є значеннями5. Вам потрібно створити словник для кожного із ваших атрибутів, а потім додайте їх за допомогою наведених вище функцій. Перше, що вам потрібно зробити — це створити 2 порожні словники, використовуючи фігурні дужки:
gender_dict = {}
relation_dict = {}
Тепер ми можемо прокрутити наш список вершин та ребер і додати відповідні елементи до кожного словника. Ми робимо це, знаючи заздалегідь позицію або індекс кожного атрибута. Оскільки наш файл lviv_network_nodes.csv добре організований, ми знаємо, що ім’я людини завжди буде першим у списку: індекс 0, оскільки в Python ви завжди починаєте підрахунок з 0. Стать людини буде індексована одиницею. Аналогічні міркування стосуються і файлу lviv_network_edges.csv. Тому ми можемо будувати наші словники так:6
for node in nodes: # Пробіжіться по списку вершин, по одному рядку за раз
gender_dict[node[0]] = node[1] # Доступіться до правильного об’єкта, додайте його до відповідного словника
for edge in edges: # Пробіжіться по списку ребер, по одному рядку за раз
relation_dict[(edge[0], edge[1])] = edge[2] # Доступіться до правильного об’єкта, додайте його до відповідного словника
Тепер у вас є набір словників, які можна використовувати для додавання атрибутів до вершин у вашому об’єкті Graph. Функції set_node_attributes та set_edge_attributes приймає три змінні: граф, до якого ви додаєте атрибут, словник пар ідентифікатор-атрибут та ім’я нового атрибута. Код для додавання ваших шести атрибутів виглядає так:
# Додайте кожен словник як атрибут вершини до об’єкта Graph
nx.set_node_attributes(G, gender_dict, 'gender')
nx.set_edge_attributes(G, relation_dict, 'relation')
Тепер усі ваші вершини мають атрибут статі, а ребра атрибут типу зв’язку і ви можете отримати до них доступ у будь-який час. Наприклад, ви можете отримати стать людей у мережі, які репрезентовані вершинами, прокрутивши їх і отримавши доступ до атрибута статі, ось так:
# Перегляньте кожну вершину, щоб отримати доступ до всіх атрибутів “стать” і виведіть їх
for n in G.nodes():
print(n, G.nodes[n]['gender'])
З цього оператора ви отримаєте вихідний рядок для кожної вершини в мережі. Це має виглядати як простий список імен і статі:
Margareta Joannis olim Winiarz ex pl. Temryczowska sbs. Haliciensis vidua female
Magister Albertus Pedianus, gener male
Catherina de Medinicze Mathiae Kusma conj., filia olim Catherinae Woythkowna qua fuit soror germana Magdae conj. Jacobi Szoszenka Ferrifabri sbs. L. female
Sophia Armena olim Grzeskonis Jakubowic Armeni cv. L. vidua female
Palachna Bildachowna Ruthena _ukiani Wasilowic conj. cv. L. female
Наведені вище кроки є звичайним методом додавання атрибутів до вершин, які ви повторно використовуватимете пізніше в уроці. Ось підсумок кодового блоку з цього розділу:
# Створіть порожній словник для кожного атрибута
gender_dict = {}
relation_dict = {}
for node in nodes: # Пробіжіться по списку вершин, по одному рядку за раз
gender_dict[node[0]] = node[1] # Доступіться до правильного об’єкта, додайте його до відповідного словника
for edge in edges: # Пробіжіться по списку ребер, по одному рядку за раз
relation_dict[(edge[0], edge[1])] = edge[2] # Доступіться до правильного об’єкта, додайте його до відповідного словника
# Додайте кожен словник як атрибут вершини до об’єкта Graph
nx.set_node_attributes(G, gender_dict, 'gender')
nx.set_edge_attributes(G, relation_dict, 'relation')
# Перегляньте кожну вершину, щоб отримати доступ до всіх атрибутів “стать” і виведіть їх
for n in G.nodes():
print(n, G.nodes[n]['gender'])
Тепер ви дізналися, як створити об’єкт Graph і додати до нього атрибути. У наступному розділі ви дізнаєтесь про різні метрики, доступні в NetworkX, і про те, як до них отримати доступ. Але розслабтеся, тепер ви вивчили основну частину коду, який вам знадобиться для решти уроку!
Метрики, доступні в NetworkX
Коли ви починаєте працювати над новим набором даних, доцільно отримати загальне уявлення про дані. Перший крок, описаний вище, це просто відкрити файли та подивитися, що всередині. Оскільки це мережа, ви знаєте, що там будуть вершини та межі, але скільки саме кожного з них? Яка інформація додається до кожної вершини або ребра?
У нашому випадку 114 ребер і 149 вершин. Ці ребра не мають напрямків (тобто між людьми є симетричний зв’язок), однак володіють додатковою інформацією про тип зв’язку. Для вершин ми знаємо їхню стать.
Ці деталі повідомляють, що ви можете робити зі своїм набором даних. Занадто мало вершин (скажімо, 15), і аналіз мережі менш корисний, ніж малювання малюнка чи читання; занадто багато (скажімо, 15 мільйонів), і вам слід почати з підмножини або знайти суперкомп’ютер.
Властивості мережі також керують вашим аналізом. Оскільки ця мережа неспрямована, ваш аналіз повинен використовувати метрики, які вимагають симетричних країв між вершинами. Наприклад, ви можете визначити, до яких спільнот потрапляють люди, але ви не можете визначити напрямкові маршрути, якими інформація може протікати в мережі (для цього вам потрібна спрямована мережа). Використовуючи симетричні ненаправлені зв’язки в цьому випадку, ви зможете знайти підспільноти та людей, які є важливими для цих спільнот, процес, який був би складнішим (хоча все ще можливим) із спрямованою мережею. NetworkX дозволяє виконувати більшість аналізів, які ви можете собі уявити, але ви повинні розуміти можливості свого набору даних і розуміти, що деякі алгоритми NetworkX більше підходять, ніж інші.
Форма мережі
Побачивши, як виглядає набір даних, важливо побачити, як виглядає мережа. Це різні речі. Набір даних — це абстрактне представлення того, якими є припущені зв’язки між об’єктами; мережа є конкретною реалізацією цих припущень. Мережа, принаймні в цьому контексті, — це те, як комп’ютер читає з’єднання, які ви закодували в наборі даних. Мережа має топологію або сполучну форму, яка може бути централізованою або децентралізованою; щільною або небагатою на зв’язки (рідкою); циклічною або лінійною. Водночас набір даних її не має, поза структурою таблиці, у якій він записаний.
Форма мережі та основні властивості дадуть вам зрозуміти, з чим ви працюєте та які аналізи здаються доцільними. Ви вже знаєте кількість вершин і ребер, але як «виглядає» мережа? Чи групуються вершини разом, чи вони однаково розподілені? Чи є складні структури, чи кожна вершина розташована вздовж прямої лінії?
Наведена нижче візуалізація, створена в інструменті візуалізації мережі Gephi, дасть вам уявлення про топологію цієї мережі.7 Ви можете створити подібний граф у Palladio, дотримуючись цього уроку.
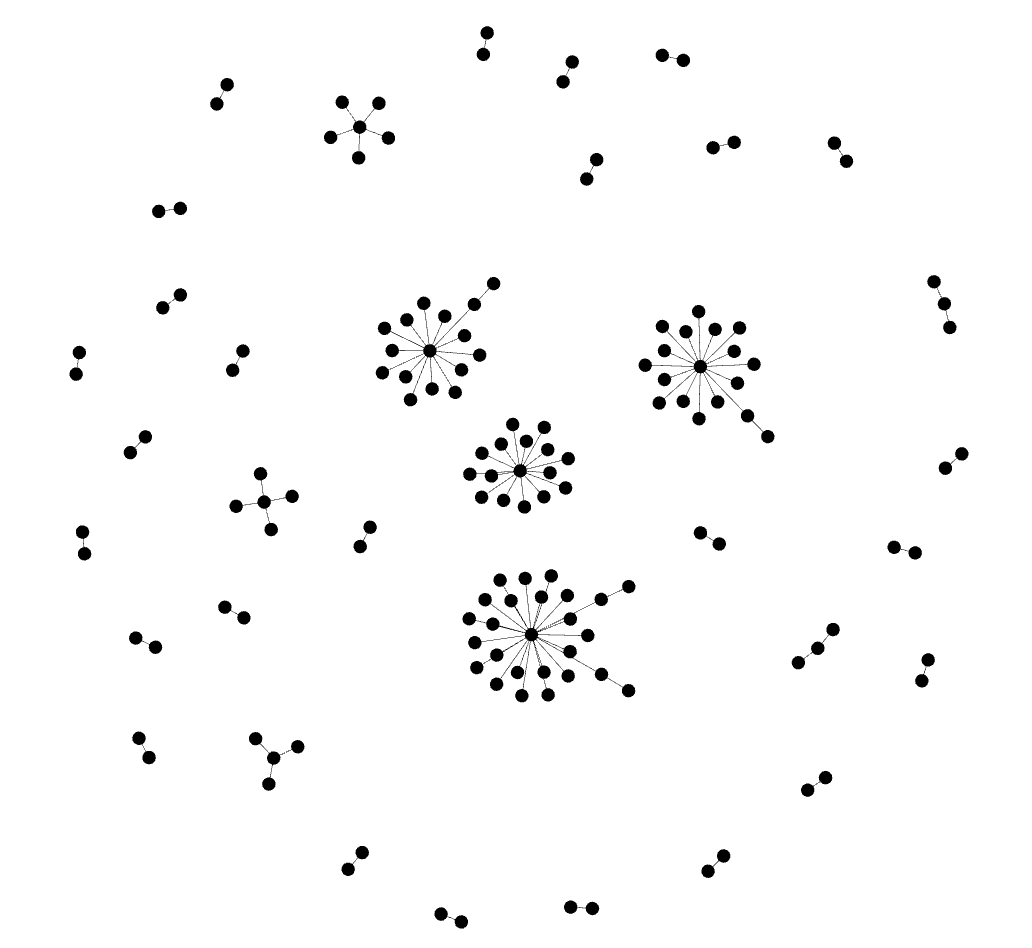
Силовий алгоритм візуалізації графу наших даних створений у Gephi
Існує багато способів візуалізації мережі, і cиловий алгоритм візуалізації графів, прикладом якого є зображення вище, є одним з найпоширеніших. Силовий алгоритм візуалізації графів намагається знайти оптимальне розміщення для вершин за допомогою розрахунку, заснованого на натягу пружин у законі Гука, який для менших графів часто створює чіткі, легкі для читання візуалізації. Візуалізація, презентована вище, показує вам, що є декілька великих компонент з’єднаних вершин та більше маленьких компонентів лише з одним або двома з’єднаннями по краях. Це досить поширена структура мережі. Знання того, що в мережі є кілька компонентів, обмежить обчислення, які ви захочете виконати в ній. Відображаючи кількість з’єднань (відому як степінь, див. нижче) як розмір вершин, візуалізація також показує, що є кілька вершин із великою кількістю з’єднань, які утримують центральний компонент пов’язаним разом. Ці великі вершини відомі як хаби, і той факт, що вони тут так чітко з’являються, дає вам підказку про те, що ви знайдете, вимірявши центральність у наступному розділі.
Візуалізація, однак, має обмежені можливості. Чим більше мереж ви опрацюєте, тим більше усвідомите, що більшість з них здаються настільки схожими, що важко відрізнити одну від іншої. Кількісні показники дозволяють відрізняти мережі, дізнаватися про їхні топології та перетворювати нагромадження вершин і ребер на те, з чого можна навчитися.
Хорошим показником для початку є щільність мережі. Це просто співвідношення фактичних ребер у мережі до всіх можливих ребер у мережі. У ненаправленій мережі, як ця, між будь-якими двома вершинами може бути одне ребро, але, як ви бачили на візуалізації, насправді присутні лише деякі з цих можливих ребер. Щільність мережі дає змогу швидко зрозуміти, наскільки тісно зв’язана ваша мережа.
І добра новина полягає в тому, що багато з цих показників потребують простих однорядкових команд у Python. З цього моменту ви можете продовжувати будувати блок коду з попередніх розділів. Вам не потрібно видаляти нічого, що ви вже ввели, і оскільки ви створили свій мережевий об’єкт G у кодовому блоці вище, усі метрики з цього моменту мають працювати правильно.
Ви можете обчислити щільність мережі, запустивши nx.density(G). Однак найкращий спосіб зробити це — зберегти свою метрику в змінній для подальшого використання та надрукувати цю змінну так:
density = nx.density(G)
print("Network density:", density)
Результатом щільності є число, тож це те, що ви побачите, коли надрукуєте значення. У цьому випадку щільність нашої мережі становить приблизно 0.0103. За шкалою від 0 до 1 це не дуже щільна мережа, яка відповідає тому, що ви бачите у візуалізації.8 0 означатиме, що зв’язків немає взагалі, а 1 вказуватиме на наявність усіх можливих ребер (ідеально підключена мережа): наша мережа знаходиться на нижній частині цієї шкали, але все ще далека від 0.
Вимірювання найкоротшого шляху дещо складніше. Він обчислює найкоротший можливий ряд вершин і ребер, які стоять між будь-якими двома вершинами, що важко побачити у візуалізаціях великих мереж. Ця міра, по суті, полягає в пошуку друзів друзів — якщо моя мати знає когось, кого я не знаю, то мама є найкоротшим шляхом між мною та цією людиною.
Щоб обчислити найкоротший шлях, вам потрібно буде передати кілька вхідних змінних (інформацію, яку ви надаєте функції Python): весь граф, вихіднну вершину і цільову вершину. Давайте знайдемо найкоротший шлях між Agnes Ganschornowa і Abraam Dawidowicz Judaeus. Оскільки ми використовували імена для унікальної ідентифікації наших вершин у мережі, ви можете отримати доступ до цих вершин (як джерело та ціль вашого шляху), використовуючи безпосередньо імена.
agnes_abraam_path = nx.shortest_path(G, source="Agnes Ganschornowa olim Joannis Ganschorn secund. nupt. vidua", target="Infidelis Abraam Dawidowicz Judaeus L.")
print("Shortest path between Agnes and Abraam:", agnes_abraam_path)
Залежно від розміру вашої мережі обчислення може зайняти деякий час, оскільки Python спочатку знаходить усі можливі шляхи, а потім вибирає найкоротший. Результатом shortest_path буде список вершин, який включає «джерело» (Agnes Ganschornowa), «ціль» (Abraam Dawidowicz Judaeus) і вершини між ними. У цьому випадку ми бачимо, що Paulus Kraus Ostiarius знаходиться на найкоротшому шляху між ними. Оскільки Paulus Kraus Ostiarius також є центром (див. степінь центральності нижче) з багатьма зв’язками, ми можемо припустити, що кілька найкоротших шляхів проходять через нього як посередника. Що це може сказати про важливість Paulus Kraus Ostiarius для їхньої соціальної мережі?
Python містить багато інструментів, які обчислюють найкоротші шляхи. Є функції для визначення довжини найкоротших шляхів, для всіх найкоротших шляхів, а також для того, чи існує шлях взагалі в документації. Ви можете використати окрему функцію, щоб дізнатися довжину шляху Agnes-Abraam, який ми щойно розрахували, або ви можете просто взяти довжину списку мінус одиницю,9 ось так:
print("Length of that path:", len(agnes_abraam_path)-1)
Існує багато мережевих показників, отриманих із довжини найкоротшого шляху. Одним із таких заходів є діаметр, який є найдовшим із усіх найкоротших шляхів. Після обчислення всіх найкоротших шляхів між кожною можливою парою вершин у мережі діаметр є довжиною шляху між двома найвіддаленішими вершинами. Цей показник розроблений, щоб дати вам уявлення про загальний розмір мережі, відстань від одного кінця мережі до іншого.
Діаметр використовує просту команду: nx.diameter(G). Однак виконання цієї команди на нашому графі призведе до повідомлення про помилку, що граф «незв’язний». Це просто означає, що ваш граф, як ви вже бачили, має більше ніж одну компоненту. Оскільки деякі вершини не мають жодного шляху до інших, неможливо знайти всі найкоротші шляхи. Погляньте ще раз на візуалізацію вашого графа:

Силовий алгоритм візуалізації графу наших даних створений у Gephi
Оскільки немає доступного шляху між вершинами одного компонента та вершинами іншого, nx.diameter() повертає помилку «незв’язний». Ви можете виправити це, спершу з’ясувавши, чи ваш граф «з’єднаний» (тобто одна компонента зв’язності), і, якщо граф не з’єднаний, знайдіть найбільший компонент і обчисліть діаметр лише для цього компонента. Ось код:
#Якщо ваш графік містить більше одного компонента, це поверне значення False:
print(nx.is_connected(G))
# Далі використайте nx.connected_components, щоб отримати список компонентів,
# згодом використайте the max() команду, щоб знайти найдовший:
components = nx.connected_components(G)
largest_component = max(components, key=len)
# Створіть «підграф» лише найбільшого компонента
# Потім обчисліть діаметр цього підграфа, як ви робили з щільністю.
subgraph = G.subgraph(largest_component)
diameter = nx.diameter(subgraph)
print("Network diameter of largest component:", diameter)
Оскільки ми взяли найбільший компонент, можна припустити, що для інших компонентів немає більшого діаметру. Таким чином, ця цифра є гарним замінником діаметра всього графа. Діаметр мережі найбільшого компонента цієї мережі дорівнює 4: існує довжина шляху 4 між двома найбільш віддаленими вершинами в мережі. На відміну від щільності, яка змінюється від 0 до 1, за одним лише цим числом важко визначити, чи 4 є великим чи малим діаметром. Для деяких глобальних показників найкраще порівняти їх із мережами подібного розміру та форми.10
Остаточний структурний розрахунок, який ви зробите в цій мережі, стосується концепції тріадичного замикання. Тріадичне замикання припускає, що якщо дві людини знають одну людину, вони, швидше за все, знають один одного. Кількість цих замкнутих трикутників у мережі можна використовувати для пошуку кластерів і спільнот індивідуумів, які знають один одного досить добре.
Один із способів вимірювання тріадного замикання називається коефіцієнтом кластеризації через цю тенденцію до кластеризації, але міра структурної мережі, яку ви дізнаєтеся, відома як транзитивність11. Транзитивність — це відношення кількості наявних трикутників до кількості всіх можливих трикутників. Можливий трикутник існує, коли одна людина знає двох людей. Отже, транзитивність, як і щільність, виражає, наскільки взаємопов’язаний граф у термінах співвідношення фактичних зв’язків до можливих. Пам’ятайте, такі вимірювання, як транзитивність і щільність, стосуються ймовірності, а не достовірності. Усі виходи вашого сценарію Python необхідно інтерпретувати, як і будь-який інший об’єкт дослідження. Транзитивність дає вам спосіб думати про всі зв’язки у вашому графі, які можуть існувати, але зараз їх немає.
Ви можете обчислити транзитивність в одному рядку так само, як ви обчислили щільність:
triadic_closure = nx.transitivity(G)
print("Triadic closure:", triadic_closure)
Так само, як і щільність, транзитивність змінюється від 0 до 1, і ви бачите, що транзитивність мережі становить 0. Це означає, що або наші дані неповні та не відображають усіх можливих стосунків серед зрізу суспільства, що ми досліджуємо або що ці дані репрезентують специфічні групи з’єднані не дружніми стосунками, а радше через торгівлю чи послуги.
Центральність
Отримавши деякі базові показники всієї структури мережі, наступним кроком буде визначити, які вершини є найважливішими у вашій мережі. У мережевому аналізі показники важливості вершини називаються показниками центральності. Тому що є багато способів підійти до питання «Які вершини є найважливішими?» існує багато різних способів обчислення центральності. Тут ви дізнаєтесь про три найпоширеніші міри центральності: степінь, міжцентральність та центральність власного вектора.
Степінь — найпростіший і найпоширеніший спосіб пошуку важливих вузлів. Степінь вершини — це сума його ребер. Якщо вершина має три лінії, що проходять від нього до інших вершин, його степінь дорівнює трійці. П’ять ребер, його степінь — п’ять. Це насправді так просто. Оскільки кожне з цих ребер завжди матиме вершину на іншому кінці, ви можете подумати про степінь як про кількість людей, з якими дана особа безпосередньо пов’язана. Вершини з найвищим степенем у соціальній мережі – це люди, які знають найбільше людей. Ці вузли часто називають концентраторами, і обчислення степеня є найшвидшим способом ідентифікації концентраторів.
Розрахунок центральності для кожної вершини в NetworkX не такий простий, як метрики для всієї мережі, наведені вище, але він все одно передбачає однорядкові команди. Усі команди центральності, які ви дізнаєтесь у цьому розділі, створюють словники, у яких ключі є вершинами, а значення – мірами центральності. Це означає, що їх можна знову додати у вашу мережу як атрибут вершини, як ви зробили в попередньому розділі. Почніть з обчислення степеня та додавання його як атрибута до вашої мережі.
degree_dict = dict(G.degree(G.nodes()))
nx.set_node_attributes(G, degree_dict, 'degree')
Ви щойно запустили метод G.degree() для повного списку вершин у вашій мережі (G.nodes()). Оскільки ви додали його як атрибут, тепер ви можете побачити степінь Paulus Kraus Ostiarius разом з іншою його інформацією, якщо ви отримаєте прямий доступ до його вершини:
print(G.nodes['Paulus Kraus Ostiarius'])
Але ці результати корисні не тільки для додавання атрибутів до об’єкта Graph. Оскільки ви вже використовуєте Python, ви можете сортувати та порівнювати їх. Ви можете використовувати вбудовану функцію sorted(), щоб відсортувати словник за його ключами або значеннями та знайти перші двадцять вершин, упорядкованих за степенем. Для цього вам знадобиться використати itemgetter, який ми імпортували на початку підручника. Використовуючиsorted і itemgetter, ви можете сортувати словник степенів таким чином:
sorted_degree = sorted(degree_dict.items(), key=itemgetter(1), reverse=True)
Тут багато чого відбувається за лаштунками, але просто зосередьтеся на трьох вхідних змінних, які ви надали sorted(). По-перше, це словник, degree_dict.items(), який потрібно відсортувати. Друге – це те, за чим сортувати: у цьому випадку елемент «1» є другим елементом у парі або значенням вашого словника. Нарешті, ви вказуєте sorted() діяти у зворотному порядку, щоб вершини з найвищим степенем були першими в списку, що є результатом перетворень. Після того як ви створили цей відсортований список, ви можете прокрутити його та використати метод «відокремлення частини списку»3, щоб отримати лише перші 20 вершин:
print("Top 20 nodes by degree:")
for d in sorted_degree[:20]:
print(d)
Як бачите, степінь Paulus Kraus Ostiarius - 23, що є відносно високим для цієї мережі. Але виведення цієї інформації про рейтинг ілюструє обмеження степеня як міри центральності. Можливо, вам не знадобилася мережа NetworkX, щоб сказати вам, що Paulus Kraus Ostiarius, був важливим. Більшість соціальних мереж матимуть лише кілька вершин дуже високого степеня, а решта – схожі, набагато нижчого степеня.12 Степінь може розповісти вам про найбільші центри, але не може сказати вам більше про решту вершин. І в багатьох випадках ті центри, про які вам розповідає (наприклад, Paulus Kraus Ostiarius або Adamus Kalinowski), не викликають особливого подиву. У цьому випадку майже всі хаби є важливими фігурами.
На щастя, існують інші показники центральності, які можуть розповісти вам не лише про хаби. Центральність власного вектора — це свого роду розширення степеня — воно розглядає комбінацію ребер вершин та ребер сусідніх вершин. Центральність власного вектора враховує чи ця вершина є хабом, як і до скількох інших хабів вона з’єднана. Він обчислюється як значення від 0 до 1: чим ближче до одиниці, тим більша центральність. Центральність власного вектора важлива для того, аби знати які вершини якнайшвидше передадуть інформацію всім іншим вершинам. Якщо ви знаєте багато людей із хорошими зв’язками, ви можете поширювати повідомлення дуже ефективно. Якщо ви користувалися Google, то ви вже дещо знайомі з центральністю власного вектора. Їхній алгоритм PageRank використовує розширення цієї формули, щоб визначити, які веб-сторінки потрапляють у верхню частину результатів пошуку.
Міжцентральність дещо відрізняється від двох інших мір тим, що вона не зважає на кількість ребер будь-якої вершини або набору вершин. Міжцентральність розглядає всі найкоротші шляхи, які проходять через певну вершину (див. вище). Щоб зробити це, він повинен спочатку обчислити всі можливі найкоротші шляхи у вашій мережі, тому майте на увазі, що обчислення міжцентральності між ними займе більше часу, ніж інші показники центральності (але це не буде проблемою в наборі даних такого розміру). Міжцентральність, яка також виражається за шкалою від 0 до 1, досить хороша для пошуку вершин, які з’єднують дві інші частини мережі. Якщо ви єдине, що з’єднує два кластери, усі зв’язки між цими кластерами мають проходити через вас. На відміну від хабу, цей вид вершин часто називають брокером. Міжцентральність — це не єдиний спосіб знайти посередництво (і інші методи є більш систематичними), але це швидкий спосіб дати вам зрозуміти, які вершини важливі не тому, що вони самі мають багато зв’язків, а тому, що вони знаходяться між групами, даючи підключення та згуртованість мережі.
Ці два показники центральності навіть простіше виконувати, ніж степінь — їм не потрібно передавати список вершин, лише граф G. Ви можете запустити їх за допомогою цих функцій:
betweenness_dict = nx.betweenness_centrality(G) # Виконайте міжцентральність
eigenvector_dict = nx.eigenvector_centrality(G) # Виконайте центральність власного вектора
# Призначте кожен атрибут у вашій мережі
nx.set_node_attributes(G, betweenness_dict, 'betweenness')
nx.set_node_attributes(G, eigenvector_dict, 'eigenvector')
Ви можете відсортувати міжцентральність (або власний вектор), змінивши назви змінних у коді сортування вище, як:
sorted_betweenness = sorted(betweenness_dict.items(), key=itemgetter(1), reverse=True)
print("Top 20 nodes by betweenness centrality:")
for b in sorted_betweenness[:20]:
print(b)
Ви помітите, що багато, але не всі, вершини з високим степенем також мають високу міжцентральність. Насправді, міжцентральність виводить двох Agnes Ganschornowa olim Joannis Ganschorn secund. nupt. vidua та Anna Lucae Woinar cv. L. conj. чиє значення було затемнене показником степеня центральності. Перевага виконання цих обчислень у Python полягає в тому, що ви можете швидко порівняти два набори обчислень. Що, якщо ви хочете знати, яка із вершин центральності з високою проміжністю мала низький степінь? Тобто: у яких проміжних вершин несподівано побачити високе значення міжцентральності? Ви можете використовувати комбінацію впорядкованих списків, наведених вище:
# Спочатку отримайте перших 20 вершин з найвищим значенням міжцентральності як список
top_betweenness = sorted_betweenness[:20]
# Потім знайдіть і виведіть їхній степінь
for tb in top_betweenness: # Пробіжіться по списку `top_betweenness`
degree = degree_dict[tb[0]] # Використайте `degree_dict`, щоб отримати доступ до степеня вершити, див. виноску 2
print("Name:", tb[0], "| Betweenness Centrality:", tb[1], "| Degree:", degree)
З цих результатів ви можете підтвердити, що деякі люди, як-от Agnes Ganschornowa olim Joannis Ganschorn secund. nupt. vidua та Anna Lucae Woinar cv. L. conj., мають високу міжцентральність, але низький степінь. Це могло означати, що ці жінки були важливими вершинами-брокерами, які з’єднували різнорідні частини графа. Ви також можете дізнатися несподівані речі про людей, яких ви вже знаєте — у цьому списку ви можете побачити, що Anna Lucae Woinar cv. L. conj. має нижчий степінь, ніж Stanislaus Anserinus, але вищу центральність між людьми. Тобто просто знати більше людей — це ще не все.
Це лише частина того, що можна зробити з мережевими показниками в Python. NetworkX пропонує десятки функцій і заходів для використання в різних комбінаціях, і ви можете використовувати Python для розширення цих заходів майже необмеженими способами. Мова програмування, як-от Python або R, надасть вам гнучкість у дослідженні вашої мережі за допомогою обчислень у спосіб, яким не можуть скористатися інші інтерфейси, дозволяючи поєднувати та порівнювати статистичні результати вашої мережі з іншими атрибутами ваших даних (наприклад, тип зв’язку, який ви додали до мережі на початку цього уроку!).
Розширений NetworkX: Виявлення спільноти за допомогою модулярності
Інша поширена річ, яку потрібно запитати про мережевий набір даних, це те, які підгрупи або спільноти входять до більшої соціальної структури. Чи є ваша мережа однією великою щасливою родиною, де всі знають усіх? Або це сукупність менших підгруп, які з’єднані лише одним або двома посередниками? Сфера виявлення спільнот у мережах покликана відповісти на ці запитання. Існує багато способів обчислення спільнот, клік і кластерів у вашій мережі, але найпопулярнішим наразі є метод модулярності. Модулярність — це міра відносної щільності у вашій мережі: спільнота (яка називається модулем або класом модулярності) має високу щільність відносно інших вершин у своєму модулі, але низьку щільність щодо вершин поза її межами. Модулярність дає вам загальну оцінку того, наскільки розбіжна ваша мережа, і цю оцінку можна використовувати для розділення мережі та перегляду окремих спільнот.13
Дуже щільні мережі часто важче розділити на окремі класи. На щастя, як ви з’ясували раніше, ця мережа є не така щільна. Фактичних з’єднань не так багато, як можливих з’єднань, і є кілька повністю від’єднаних компонентів. Варто розділити цю небагату на зв’язки мережу на модулі і перевірити, чи має результат історичний та аналітичний сенс.
Виявлення спільноти та розділення в NetworkX вимагає трохи більше налаштувань, ніж деякі інші показники. Є деякі вбудовані підходи до виявлення спільноти (наприклад, мінімальне скорочення, але модулярність не включена в NetworkX). На щастя, є додатковий модуль python, який ви можете використовувати з NetworkX, який ви вже встановили та імпортували на початку цього уроку. Ви можете прочитати повну документацію щодо всіх функцій, які він пропонує, але для більшості цілей виявлення спільноти вам знадобиться лише best_partition():
communities = community.greedy_modularity_communities(G)
Метод greedy_modularity_communities() намагається визначити кількість спільнот, відповідних для графа, і групує всі вершини в підмножини на основі цих спільнот. На відміну від центральних функцій, наведений вище код не створить словник. Замість цього він створює список спеціальних «заморожених» об’єктів (подібних до списків). Для кожної групи є один набір, і набори містять імена людей у кожній групі. Щоб додати цю інформацію до вашої мережі вже відомим способом, ви повинні спочатку створити словник, який позначатиме кожну особу числовим значенням для групи, до якої вона належить:
modularity_dict = {} # Створіть пустий словник
for i,c in enumerate(communities): # Перегляньте список спільнот, відстежуючи номер спільноти
for name in c: # Перегляньте кожного члена спільноти
modularity_dict[name] = i # Створіть запис у словнику для людини, де значенням є те, до якої групи вона належить
# Тепер ви можете додати інформацію про модулярність, як ми робили з іншими показниками
nx.set_node_attributes(G, modularity_dict, 'modularity')
Як завжди, ви можете комбінувати ці заходи з іншими. Наприклад, ось як знайти вершини центральності власного вектора з найвищим у класі модулярності 0 (перший):
# Спочатку отримайте список лише вершин цього класу
class0 = [n for n in G.nodes() if G.nodes[n]['modularity'] == 0]
# Потім створіть словник центральності власних векторів цих вершин
class0_eigenvector = {n:G.nodes[n]['eigenvector'] for n in class0}
# Потім відсортуйте цей словник і виведіть перші 5 результатів
class0_sorted_by_eigenvector = sorted(class0_eigenvector.items(), key=itemgetter(1), reverse=True)
print("Modularity Class 0 Sorted by Eigenvector Centrality:")
for node in class0_sorted_by_eigenvector[:5]:
print("Name:", node[0], "| Eigenvector Centrality:", node[1])
Використання центральності власного вектора як рейтингу може дати вам уявлення про важливих людей у цьому класі модулярності. Трохи покопавшись, ми можемо виявити, що існують причини (жінки звертались за послугами до Paulus Kraus Ostiarius аби він представляв їх у суді), які об’єднують цю групу людей. Це свідчить про те, що модулярність, ймовірно, працює належним чином.
У менших мережах, подібних до цієї, звичайним завданням є пошук і перелік усіх класів модулярності та їхніх членів14. Ви можете зробити це, пройшовшись по списку communities:
for i,c in enumerate(communities): # Перегляньте список спільнот
if len(c) > 2: # Відфільтруйте класи модулярності з 2 або менше вершинами
print('Class '+str(i)+':', list(c)) # Виведіть класи та їхніх учасників
Зауважте, що в наведеному вище коді ви відфільтровуєте будь-які класи модулярності з двома або меншою кількістю вершин у рядку, якщо len(c) > 2. З візуалізації ви пам’ятаєте, що було багато маленьких компонентів мережі лише з двома вершинами. Модулярність знайде ці компоненти та розглядатиме їх як окремі класи (оскільки вони не пов’язані ні з чим іншим). Відфільтрувавши їх, ви отримаєте краще уявлення про більші класи модулярності в головному компоненті мережі.
Працюючи лише з NetworkX, ви далеко зайдете, і ви зможете дізнатися багато про класи модулярності, просто працюючи безпосередньо з даними. Але ви майже завжди захочете візуалізувати свої дані (і, можливо, виразити модулярність у вигляді кольору вершини). У наступному розділі ви дізнаєтеся, як експортувати дані NetworkX для використання в інших програмах.
Експорт даних
NetworkX підтримує дуже велику кількість форматів файлів для експорту даних. Якщо ви хочете експортувати відкритий текстовий список ребер для завантаження в Palladio, для цього є зручна обгортка. Часто в Six Degrees of Francis Bacon експортують дані NetworkX у спеціалізований формат JSON D3 для візуалізації в браузері. Ви навіть можете експортувати свій граф як Pandas датафрейм, якщо ви хочете запустити більш розширені статистичні операції. Існує багато варіантів, і якщо ви старанно додавали всі свої показники назад у свій об’єкт Graph як атрибути, усі ваші дані буде експортовано одним махом.
Більшість параметрів експорту працюють приблизно однаково, тому в цьому підручнику ви дізнаєтеся, як експортувати дані у формат GEXF Gephi. Експортувавши файл, ви можете завантажити його безпосередньо в Gephi для візуалізації.
Експорт даних часто виконується простою однорядковою командою. Все, що вам потрібно вибрати, це ім’я файлу. У цьому випадку ми будемо використовувати lviv_network.gexf. Для експорту введіть:
nx.write_gexf(G, 'lviv_network.gexf')
Ось і все! Коли ви запускаєте свій сценарій Python, він автоматично розміщує новий файл GEXF у тому ж каталозі, що й ваш файл Python.15
Нарис висновків
Опрацювавши та переглянувши масив мережевих показників у Python, ви тепер маєте докази, на основі яких можна висунути аргументи та зробити висновки щодо цієї мережі міщан у ранньомодерному Львові. Ви знаєте, наприклад, що мережа має відносно низьку щільність, що свідчить про слабкі зв’язки та/або неповні вихідні дані. Ви знаєте, що спільнота організована навколо кількох непропорційно великих центрів. Що ще корисніше, ви знаєте про жінок із відносно низьким степенем, як-от Agnes Ganschornowa olim Joannis Ganschorn secund. nupt. vidua та Anna Lucae Woinar cv. L. conj., які (внаслідок високої центральності між ними) могли діяти як брокери, з’єднуючи кілька груп. Нарешті ви дізналися, що мережа складається з декількох великих компонент та багатьох дуже маленьких. Завдяки метаданим, які ви додали до своєї мережі, у вас є інструменти для подальшого вивчення цих показників і потенційного пояснення деяких структурних особливостей, які ви ідентифікували.
Ми хочемо, щоб кожен із цих висновків спонукав до додаткових досліджень, і не був крапкою чи доказом. Аналіз мережі — це набір інструментів для постановки цільових запитань про структуру зв’язків у наборі даних, і NetworkX надає відносно простий інтерфейс для багатьох поширених методів і показників. Мережі — це корисний спосіб розширити ваше дослідження в групі, надаючи інформацію про структуру спільноти, і ми сподіваємося, що цей урок надихне вас використовувати ці показники для збагачення ваших власних досліджень і вивчення гнучкості мережевого аналізу за межами візуалізації.
-
У багатьох (але не у всіх) випадках
pipабоpip3буде встановлено автоматично з Python 3. ↩ -
У деяких інсталяціях потрібно лише вводити
pipбез «3», але в Python 3pip3є найпоширенішим. Якщо одне не працює, спробуйте інше! ↩ -
Існує кілька методів в Pythoni, які використовують цей код. Перший — це списковий вираз, які вбудовують цикли (
for n in nodes) для створення нових списків (у дужках), наприклад:new_list = [item for item in old_list]. Другий — це частина списку, яка дозволяє вам розділити або «нарізати» список. Нотація нарізки списку[1:]приймає все, крім першого елемента в списку. 1 вказує Python починати з другого елемента в списку (у Python ви починаєте відлік з 0), а двокрапка вказує Python обрати все до кінця списку. Оскільки перший рядок в обох цих списках є рядком заголовка кожного файлу CSV, ми не хочемо, щоб ці заголовки включалися в наші дані. ↩ ↩2 -
У попередній версії NetworkX можна було отримати трохи більше інформації за допомогою функції
nx.info(G), однак нещодавньо її функціонал забрали, а аналогу не додали. ↩ -
Словники — це вбудований тип даних у Python, який складається з пар ключ-значення. Вважайте ключ терміном у словнику, а значення – його визначенням. Ключі мають бути унікальними (тільки по одному для кожного словника), але значення можуть бути будь-якими. Словники представлені фігурними дужками з ключами та значеннями, розділеними двокрапками:
{key1:value1, key2:value2, ...}. Словники є одним із найшвидших способів зберігати значення, які, як ви знаєте, знадобляться вам пізніше. Насправді об’єкт NetworkX Graph сам по собі складається з вкладених словників. ↩ -
Зверніть увагу, що цей код використовує дужки двома способами. Він використовує числа в дужках для доступу до певних індексів у списку вершин (наприклад, стать у
node[1]), але також використовує дужки для призначення ключа (завждиnode[0], ID) будь-якому з наші порожні словники:dictionary[key] = value. Зручно! ↩ -
Щоб спростити, перед початком роботи ми видалили з набору даних будь-які вершини, які не пов’язані з іншими. Це було зроблено лише для того, щоб зменшити безлад, але також дуже часто можна побачити багато цих окремих вершин у вашому середньому мережевому наборі даних. ↩
-
Але майте на увазі, що це щільність усієї мережі, включно з тими непов’язаними компонентами, які плавають на орбіті. Там є багато можливих зв’язків. Якщо взяти щільність лише найбільшого компонента, ви можете отримати зовсім інше число. Ви можете зробити це, знайшовши найбільший компонент, як ми покажемо вам у наступному розділі про діаметр, а потім застосувавши той самий метод щільності лише для цього компонента. ↩
-
Тут, ми беремо довжину списку мінус один, тому що нам потрібна кількість ребер (або кроків) між перерахованими тут вершинами, а не кількість вершин. ↩
-
Основний спосіб такого порівняння — створити випадкові графи однакового розміру, щоб побачити, чи відрізняються показники від норми. NetworkX пропонує безліч інструментів для створення випадкових графів. ↩
-
Чому це називається транзитивністю? Можливо, ви пам’ятаєте властивість транзитивності з геометрії середньої школи: якщо A=B і B=C, A має дорівнювати C. Подібним чином, у тріадному замиканні, якщо особа A знає особу B, а особа B знає особу C, то особа A, ймовірно, знає особа С: отже, транзитивність. ↩
-
Ті з вас, хто має досвід у статистиці, помітять, що степінь у соціальних мережах зазвичай відповідає степеневому закону, але це не є ані незвичайним, ані особливо корисним. ↩
-
Хоча ми не будемо розглядати це в цьому уроці, зазвичай доцільно спочатку отримати глобальну оцінку модулярності, щоб визначити, чи навчитеся ви чогось, розділивши свою мережу відповідно до модулярності. Щоб побачити загальну оцінку модулярності, візьміть спільноти, які ви розрахували за допомогою
communities = community.best_partition(G)і запустітьglobal_modularity = community.modularity(communities, G). Тоді простоprint(global_modularity). ↩ -
У великих мережах списки, ймовірно, будуть нерозбірливо довгими, але ви можете отримати уявлення про всі класи модулярності одночасно, візуалізувавши мережу та додавши колір до вершин на основі їх класу модулярності. ↩
-
Кожен формат файлу, який можна експортувати, також можна імпортувати. Якщо у вас є файл GEXF від Gephi, який ви хочете помістити в NetworkX, ви повинні ввести
G = nx.read_gexf('some_file.gexf'). ↩